In data-intensive applications, it is advantageous to perform partial processing close to the data and transmit partial results to the central processor instead of the raw data. When the communication medium is noisy, it is necessary to mitigate the degradation in the model’s accuracy.
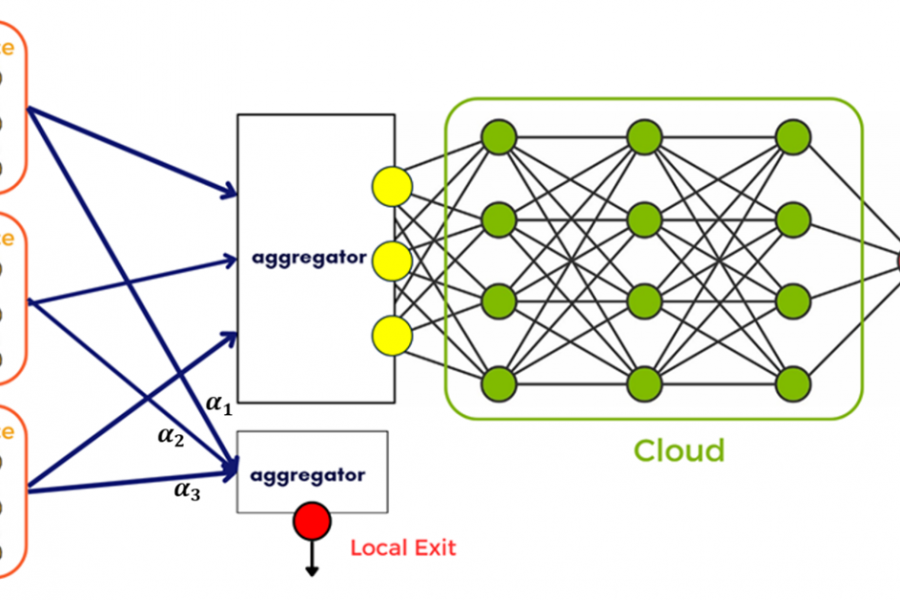
In this project, we address the issue of reduced accuracy in DDNN models due to noise in the communication channel that transmits information from end devices (to the local aggregator or the cloud).
This project’s objective is to improve the predictor’s accuracy under noisy channel conditions by finding an optimal method for selecting aggregation weights. We focus on classification problems for a finite number of classes, where each end device is a Deep Neural Network (DNN) that performs local computation and based on confidence in those computations, it is determined if the sample should exit at that point.
The project aims to find vector : optimal weights for average pooling aggregation (weighted average), by minimizing the mismatch probability between noisy prediction and the noiseless one. This minimization is accomplished through a gradient descent algorithm. Upon analyzing the results, we successfully developed an algorithm to find these weights and achieved excellent results, establishing this method as a competitive aggregation approach for high performance in local exit.

